Elettrotecnica - Trasformazione da stella a triangolo in regime permanente continuo
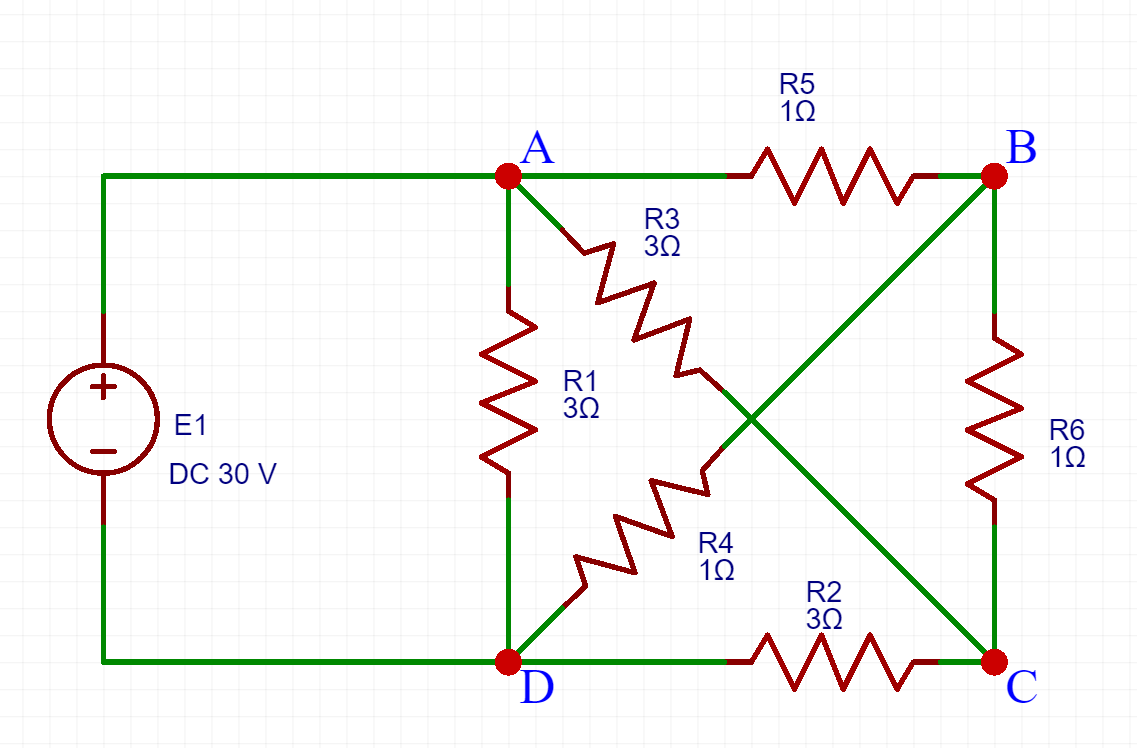
Ripropongo un semplice esercizio sulla trasformazione da stella a triangolo in continua svolto all’università. Le trasformazioni triangolo -> stella e stella -> triangolo sono utili nella semplificazione del circuito e quindi ad una più agevole risoluzione.
In regime permanente continuo. Determinare potenza erogata dal generatore e la resistenza equivalente vista ai capi del generatore.
$$P_{E1} = ?$$ $$R_{EQ} = ?$$
Rapidamente individuiamo il centro stella in B, se trascinate mentalmente il nodo b all’interno del triangolo ADC anche graficamente diventa facilmente individuabile. La strategia risolutiva quindi si baserà sulla trasformazione da stella a triangolo poiché successivamente avremo da svolgere semplicemente dei paralleli per trovare la resistenza equivalente richiesta.
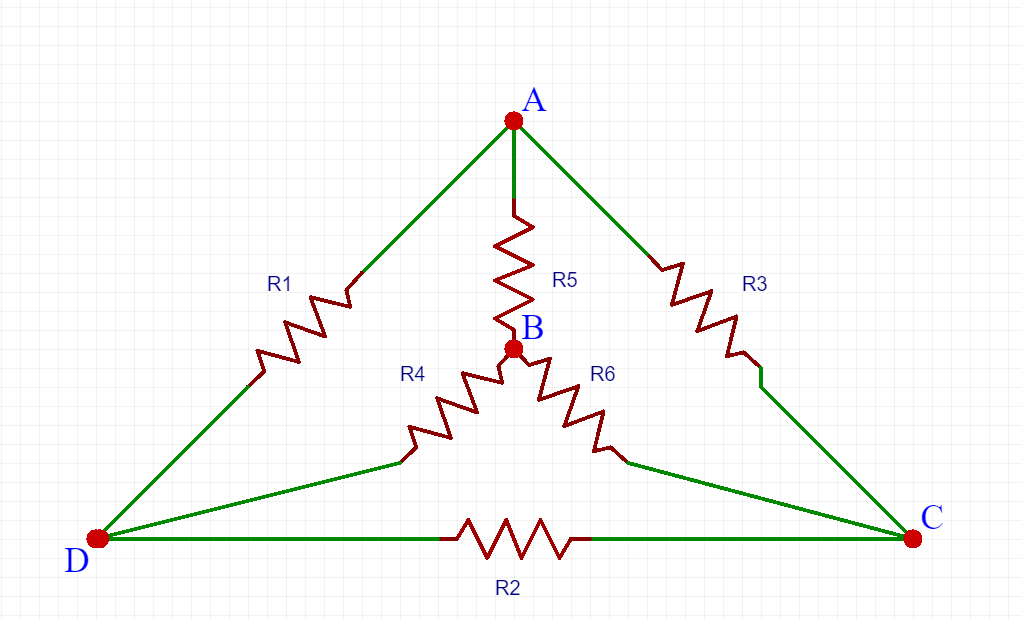
Utilizziamo la trasformazione stella triangolo sulla stella di centro B.
Quindi dalle eguaglianze:
$$R_{AD} = {{R_{5}R_{4}+R_{4}R_{6}+R_{5}R_{6}}\over{R_{6}}}$$
Avendo $R_{4}=R_{5}=R_{6}=1\Omega=R$
$$R_{AD} = R_{DC} = R_{AC} ={{R^2+R^2+R^2}\over{R}} = 3R = 3\Omega$$
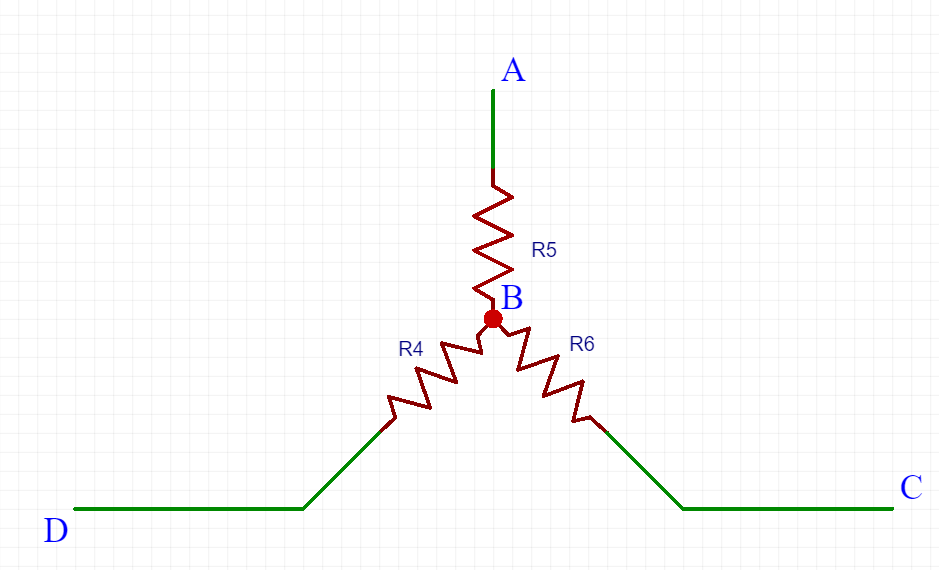
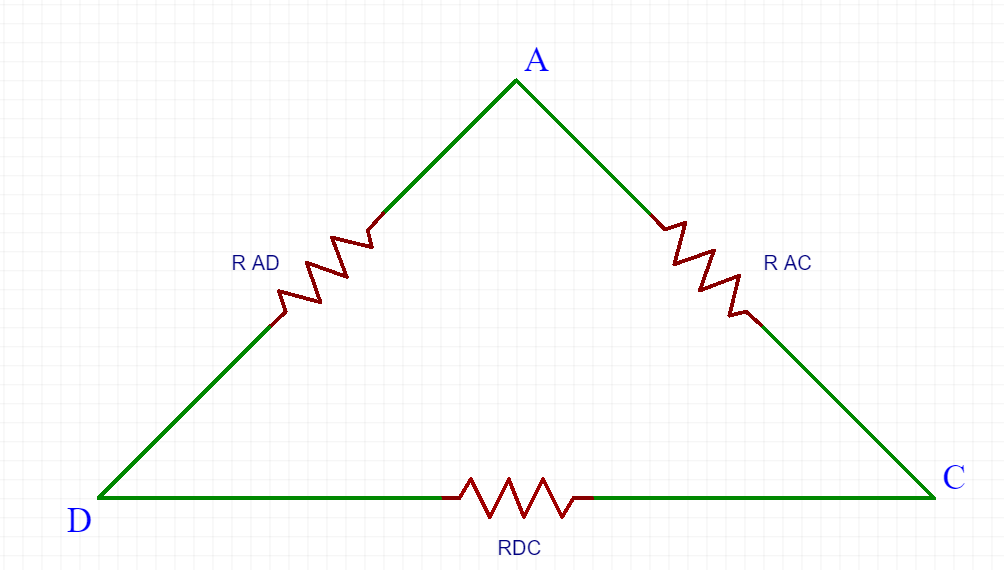
Ricavando dunque i due trinagolo.
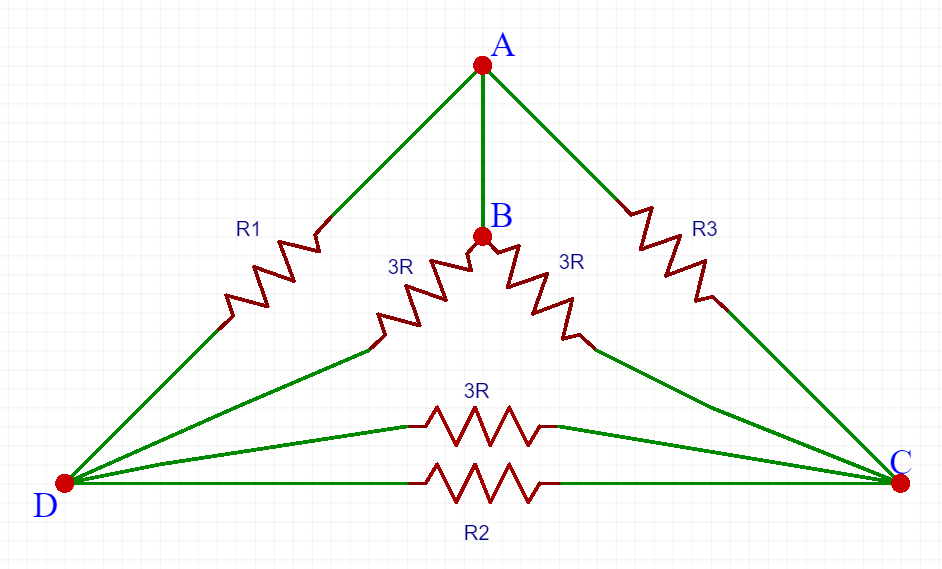
Effettuo i paralleli:
$$R_{AD'} = R_{DC'} = R_{AC'} = R_{1} || 3R = {{3 * 3}\over{9}} = 1.5\Omega$$
Circuito Risultante
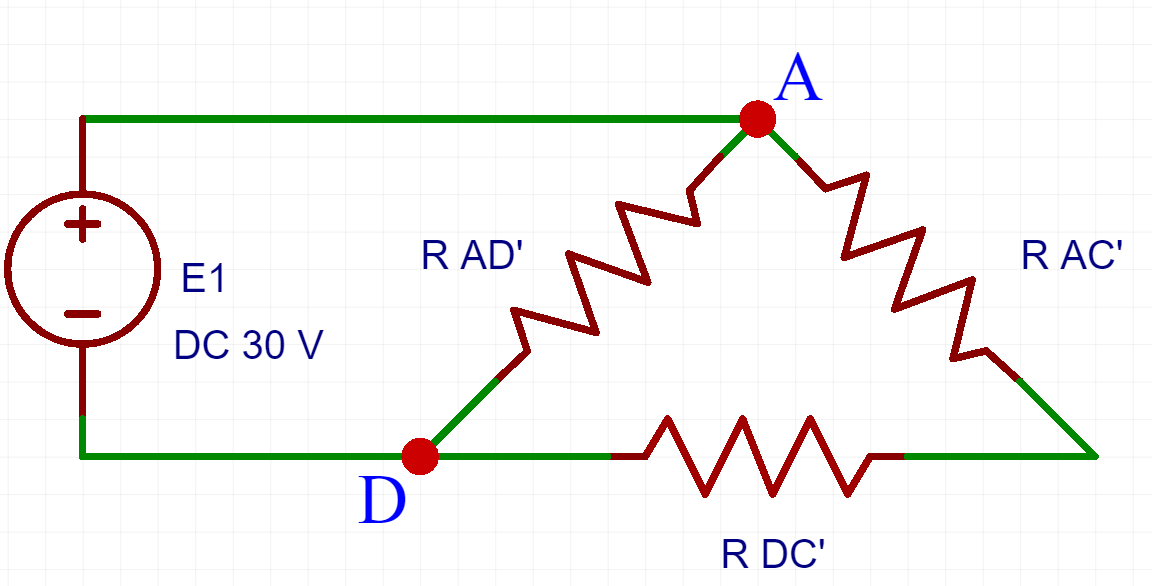
Svolgo la serie con il parallelo per trovare la resistenza equivalente.
$$R_{SERIE} = R_{AC'} + R_{DC'} = 3\Omega$$
$$R_{EQ} = R_{AD} || R_{SERIE} = {{1,5 * 3}\over{1,5+3}} = 1\Omega $$
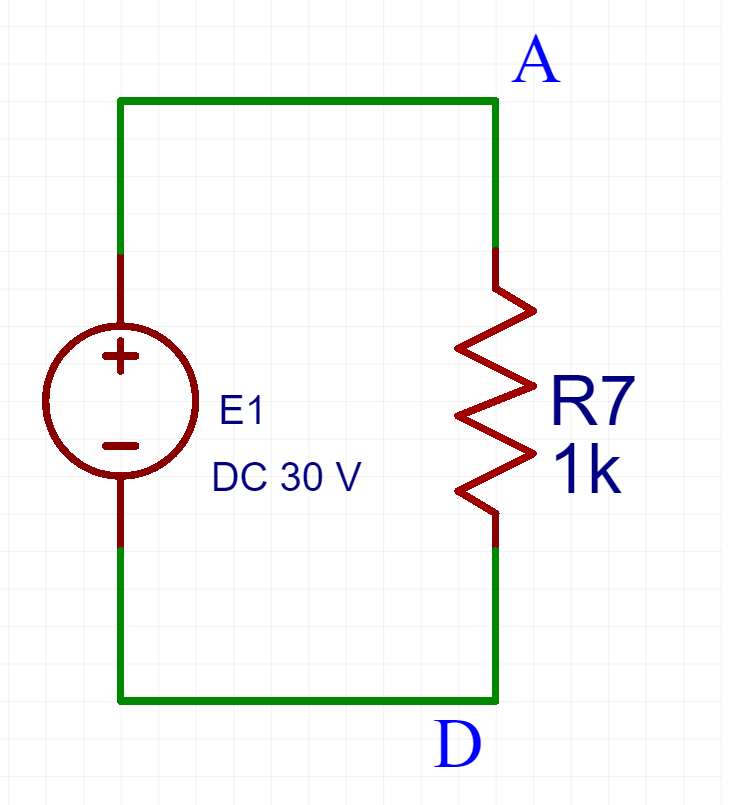
Troviamo la corrente e la potenza
$$I = {{E_{1}}\over{R_{EQ}}} = 30A$$
$$P_{E_{1}} = 30 * 30 = 900W $$

