Elettrotecnica - Fasore di tensione applicando il metodo dei nodi
Un piccolo esercizio sull’utilizzo del metodo dei nodi per determinare il fasore di tensione tra 2 morsetti.
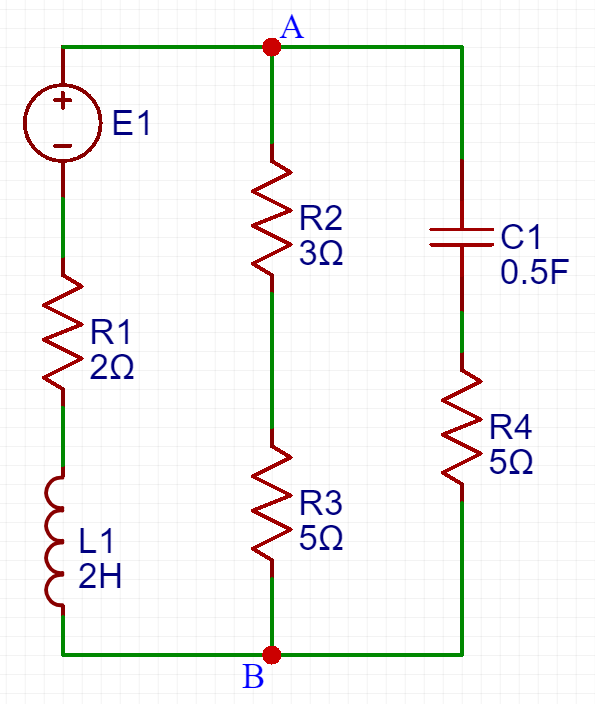
Un piccolo esercizio sull’utilizzo del metodo dei nodi per determinare il fasore di tensione tra 2 morsetti.
Traccia Determinare il fasore di tensione tra i morsetti A e B in regime permanente sinusoidale..
Avendo:
$$E_{1} = 20\sqrt{2}\cos{(\omega-\frac{\pi}{4})} $$$$f = \frac{1\pi}{\pi} Hz $$
Come primo step trasformo le varie parti nel dominio della pulsazione.
$$\omega = 2\pi \frac{1}{\pi} = 2 \frac{rad}{s} $$
$$E_{1}' = 20(\cos{(-\frac{\pi}{4})} + j\sin{(-\frac{\pi}{4})}) = 14.142 -j14.142 $$
$$L_{1}' = j\omega L_{1} = j4 $$
$$C_{1}' = -\frac{j}{\omega C_{1}} = -\frac{j}{\omega 0.5} = -j $$
Utilizzo il metodo dei nodi per determinare il fasore di tensione fra i morsetti A e B. Essendo questa rete composta dai soli nodi A e B la soluzione sarà un unica equazione ( poichè la soluzione è data da n-1 equazioni, dove n è il numero dei nodi del circuito )
$$V_{AB} = \frac{\frac{E_{1}'}{R_{1}+L_{1}'}} {\frac{1}{R_{1}+L_{1}'} + \frac{1}{R_{2}+R_{3}} + \frac{1}{C_{1}'+R_{4}}} = 0.47-j9.98 V $$
Per i calcoli, con l'introduzione di soluzione a numeri complessi, consiglio l'utilizzo di una texas o di una buona calcolatrice che rende il lavoro più agevole sulla parte immaginaria.

